Life Insurance Policy Search By Social Security Number
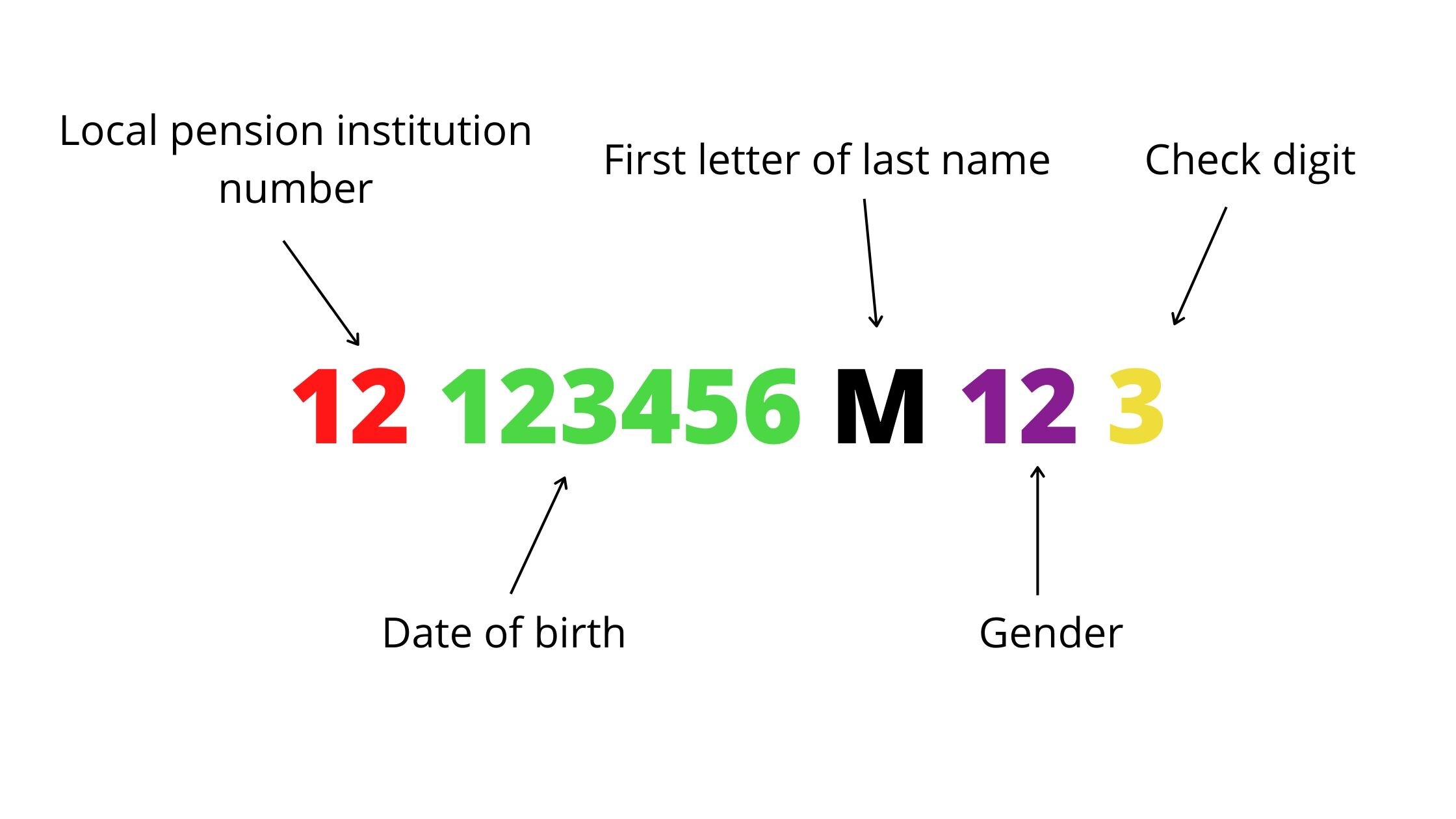
Sozialversicherungsnummer: What Is It and How Can I Get My Number …
x

How to find your policy number on insurance card – Profvalue Blog

Sozialversicherungsnummer: What Is It and How Can I Get My Number …

How to find your policy number on insurance card – Profvalue Blog